Finding, isolating, and solving an algorithm challenge in a real application

A client raised an issue that their batch delete from the Redis cache was too slow. Although initially, it was assumed Redis was at fault, it turned out that the application’s algorithm was responsible. This is the systematic approach our team followed to find, isolate, and solve the performance challenge.
Initial Debugging — Hunting Down Bottlenecks

Before profiling, initial hypotheses were formed about potential bottlenecks. However, the real value lay in scientifically confirming these suspicions with a profiler, identifying where most of the processing time was spent, and applying targeted fixes.
In this case, profiling showed that Redis deletion took only 5 seconds out of the 4-minute total response time, indicating the need to look deeper into the application logic.
Profiling
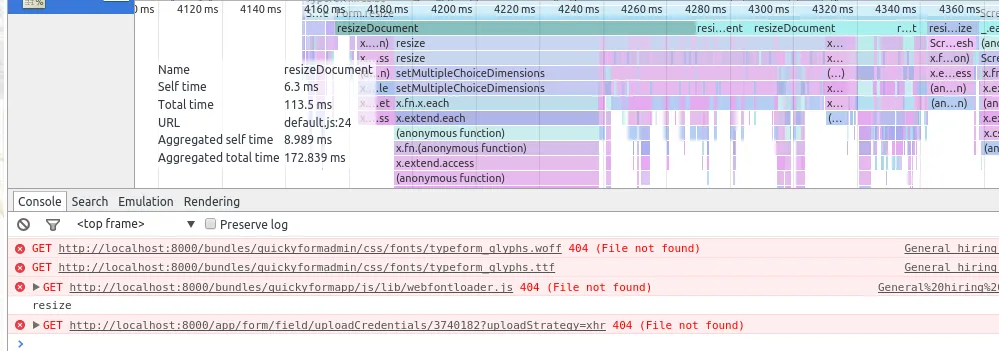
Using the profiler, it became clear that one function was responsible for over 90% of the time spent during processing.
The profiler results showed:
Method 1: 90%
Method 2: 3%
Method 3: 3%
Method 4: 3%

The Bottleneck

This highlighted method’s role was to remove keys from a list of strings based on whether they started with any of the prefixes from another collection.
For example, given keys:
- a
- ab
- abc
- abcd
- bcd
- bcdf
- bdcf
and prefixes to remove:
- “ab”
- “bcdf”
after filtering, only “a” and “bdcf” remain.
If we use a simple approach to achieve this goal, we can do something like:

The challenge was that for each key, the code looped through every prefix, resulting in
O(keys * prefixes) complexity. With 34,000 keys and 27,000 prefixes, this equated to 917,000,000 iterations—a heavy computational load.
O(34000 * 27000) = 917,000,000 iterations
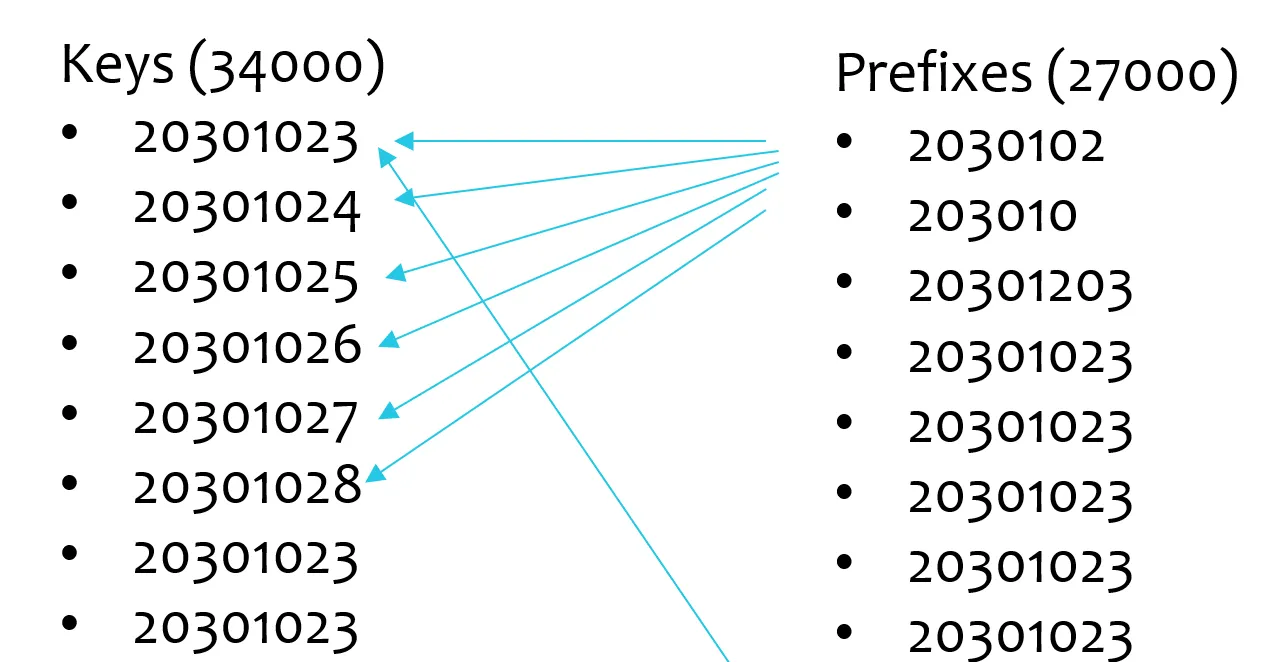
What is O(keys * prefixes)
Big O notation helps describe the computational complexity of algorithms. In this scenario, each prefix had to be checked against each key, leading to exponential growth in processing time.
Back to the Problem
Typically, challenges like removing multiple keys from an array can be addressed with hashsets or dictionaries, which have O(1) deletion time. Unfortunately, since the problem was about prefixes and not exact matches, this was not a straightforward solution.
Example
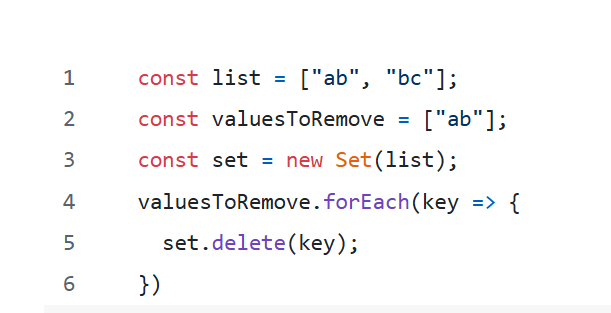
This fixes the problem because to delete from the Set is O(1), so we only have to iterate over the keys list once to build the Set, then once in the keys to remove. Bringing us to:
Big O(keys + prefixes)
However, in this scenario, a straightforward solution such as a hashset or dictionary was not applicable due to the need for prefix-based matching. This presented a classic algorithmic challenge, akin to those found on platforms like LeetCode. Nevertheless, we drew inspiration from how sets optimize deletion operations and considered whether we could index the data to reduce the cost of lookups. After conducting thorough analysis and whiteboarding different approaches, our team developed a viable indexing strategy. For illustration, consider a set of keys like:
And this prefixes to remove:
We can create a tree based on each letter of the keys:

When checking if a key starts with a given prefix, the algorithm traverses the tree to the final node corresponding to the prefix. It then removes the node and all of its child nodes, effectively reducing the time complexity to:
O(keys + prefixes)
O(34000 + 27000) = 61,000 instead of
O(34000 * 27000) = 917,000,000
Results
Before, the response time took 1.8 minutes for the whole endpoint; after this change, it went to 6 seconds. It’s a massive difference in algorithm efficiency. Furthermore, it effectively converts from exponential to linear:
Testing validated the improvement: the initial approach took 12.2 seconds, while the tree-based solution ran in only 65 milliseconds.
Conclusion
Key takeaways include:
1 — Use scientific profiling to identify the actual bottleneck.
2 — Practice and familiarity with algorithms prepare you for challenges like this.
3 — Developing a strong understanding of Big O notation helps quickly identify inefficient patterns.
This project showcased how turning an exponential problem into a linear one through algorithmic restructuring can deliver exceptional performance results for real-world applications.